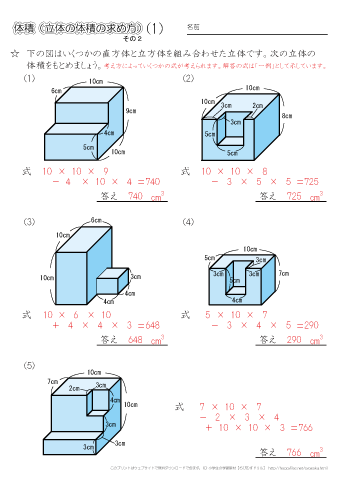
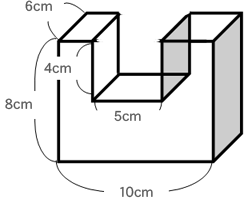
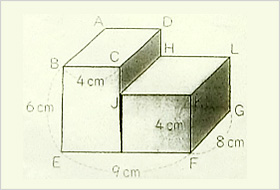
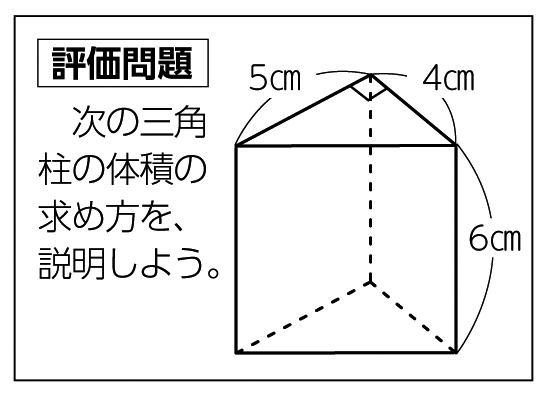
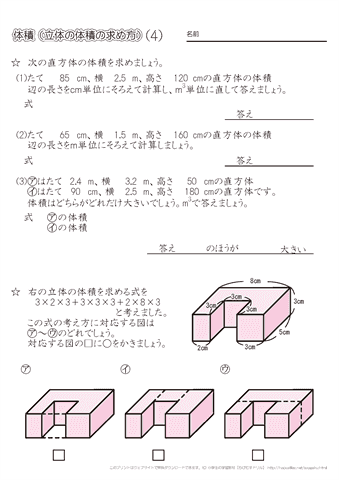
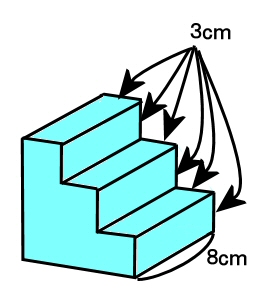
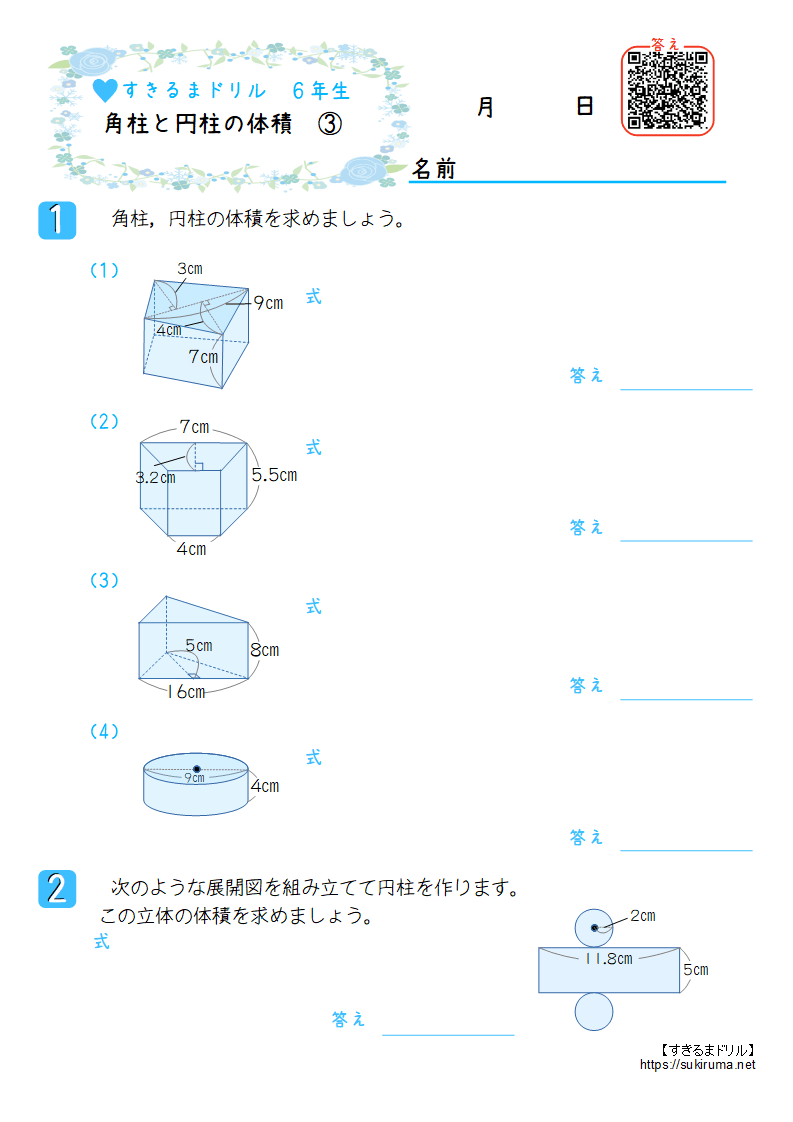
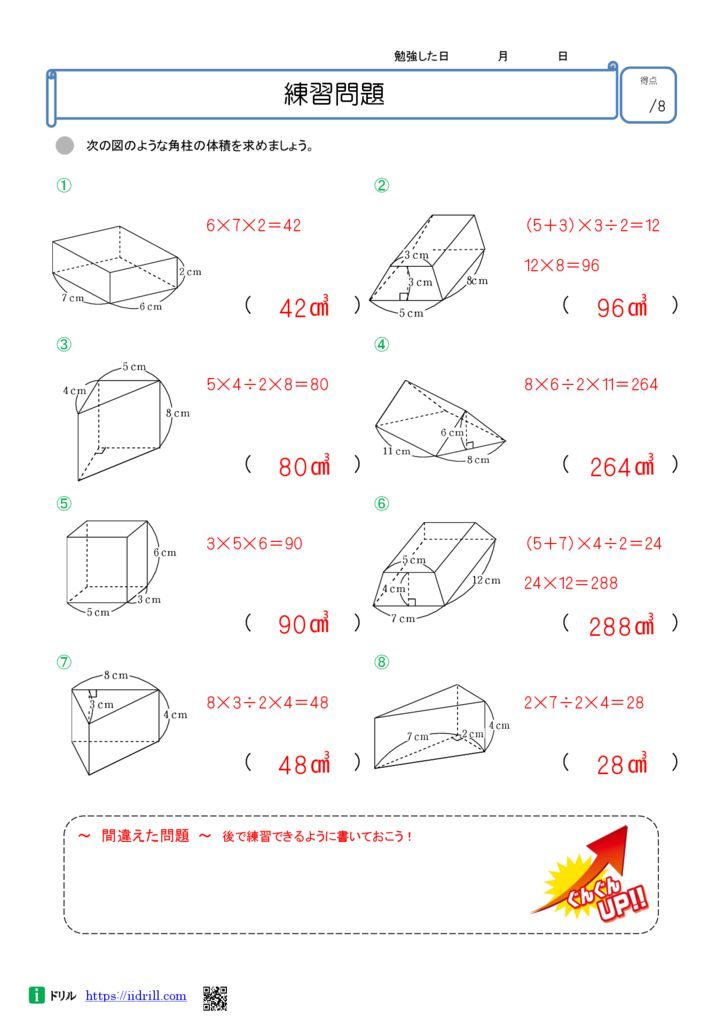
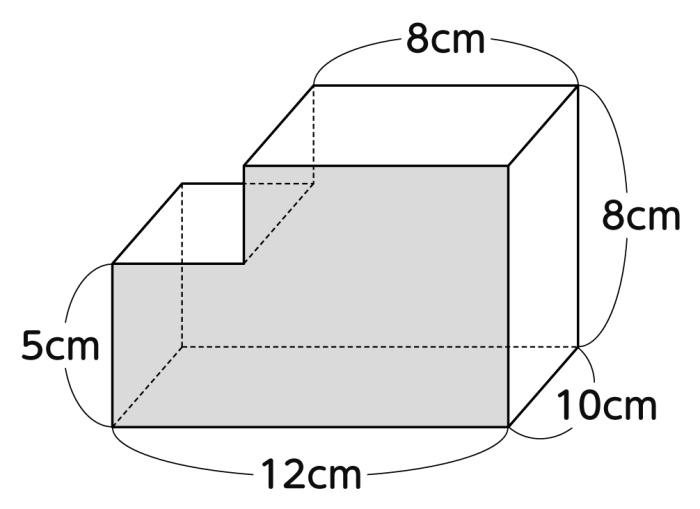
《立体の体積の求め方》 求める立体は①と②があわさって出来た立体であることから、①の直方体の体積+②の立方体の体積で求めることが出来ます。 ①の直方体の体積=8×8×4=256(cm³) ②の立方体の体積=4×4×4=64(cm³)
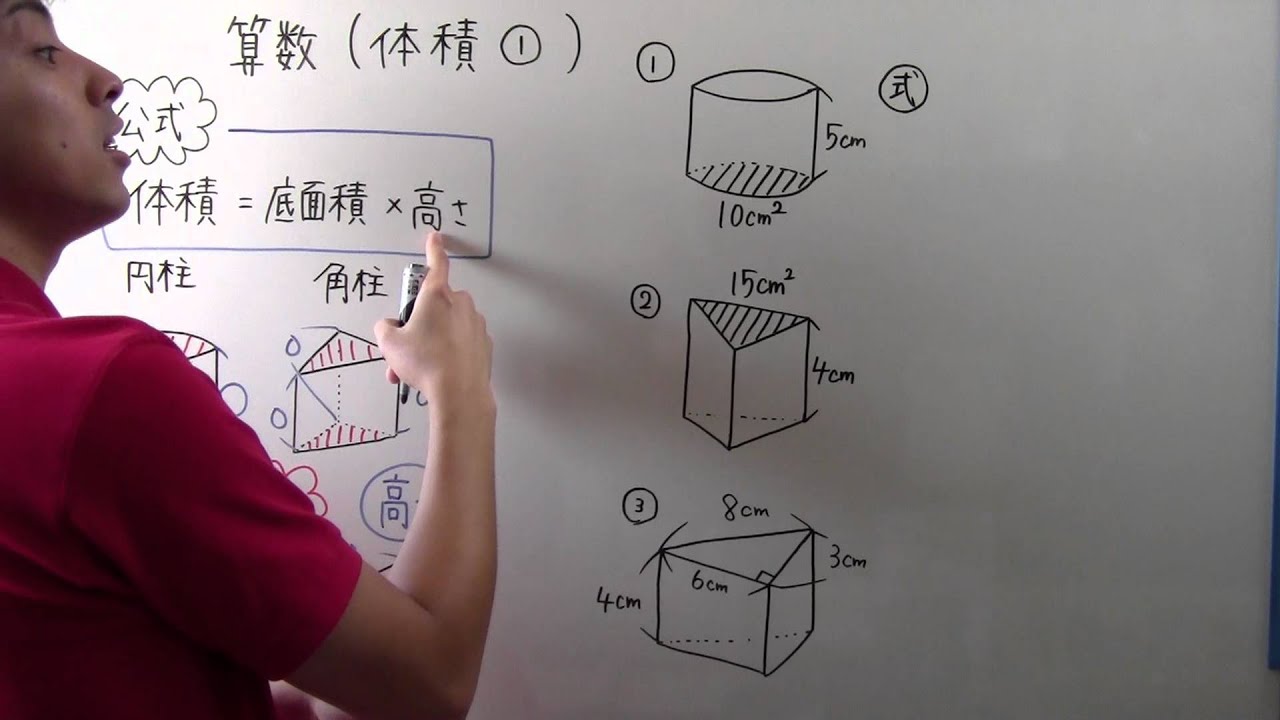
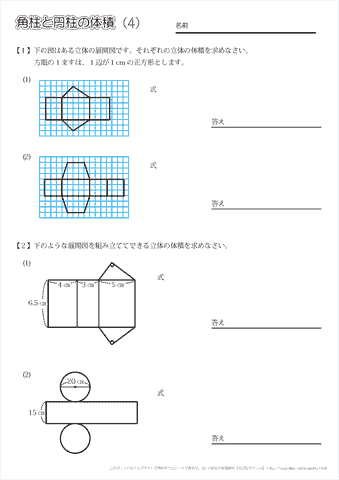
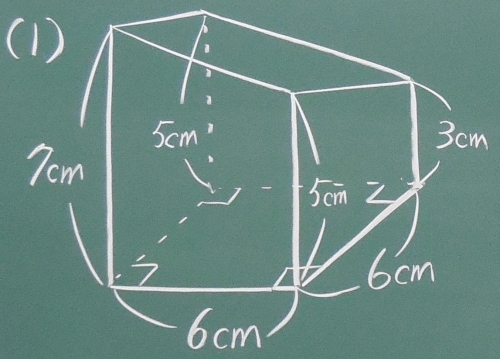
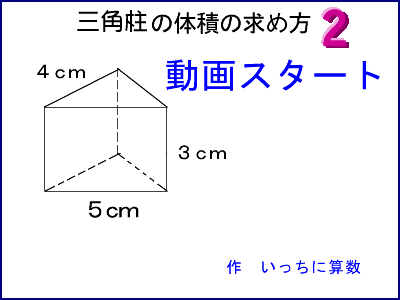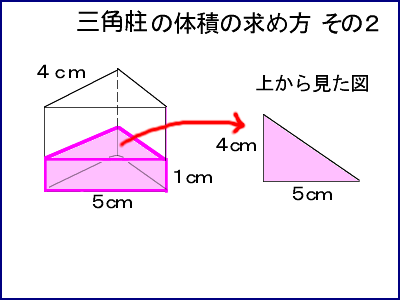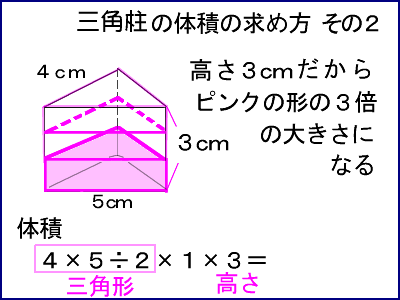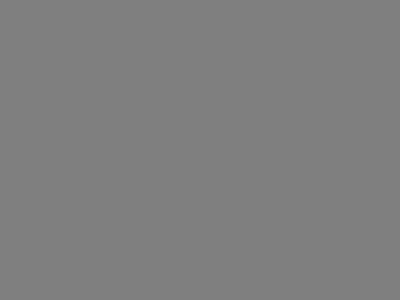
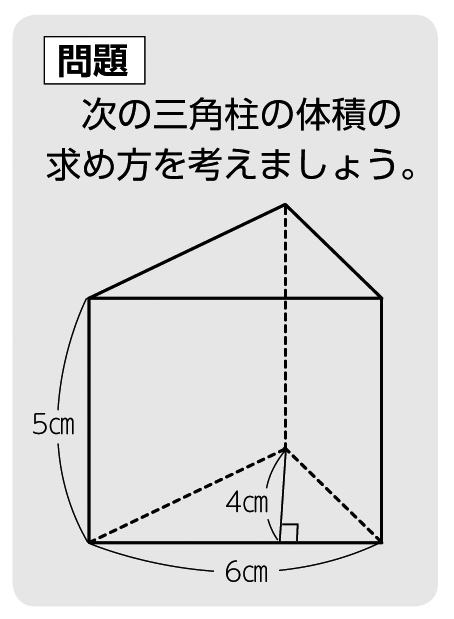
立体の体積の求め方 小6- 中学数学球の体積の求め方の公式を1発で覚える方法 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方 三角柱の体積の求め方は 「底面積 × 高さ」でしたね。 底面積は 4 × 4 × 1 2 = 8 よって、三角柱の体積は 8 × 8 = 64 体積は 64( c m 3 ) となります。 続いて、 三角柱の表面積の公式は 「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた 8 c m 2
立体の体積の求め方 小6のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「立体の体積の求め方 小6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
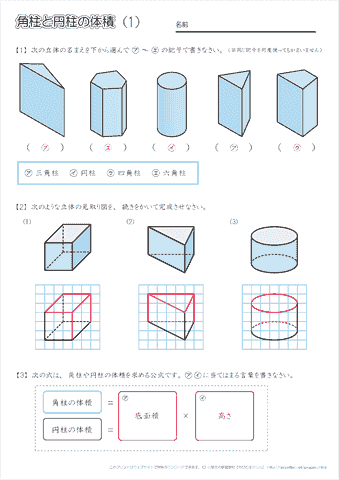
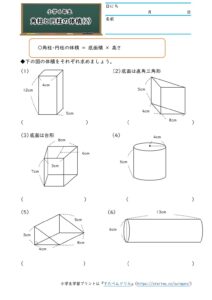
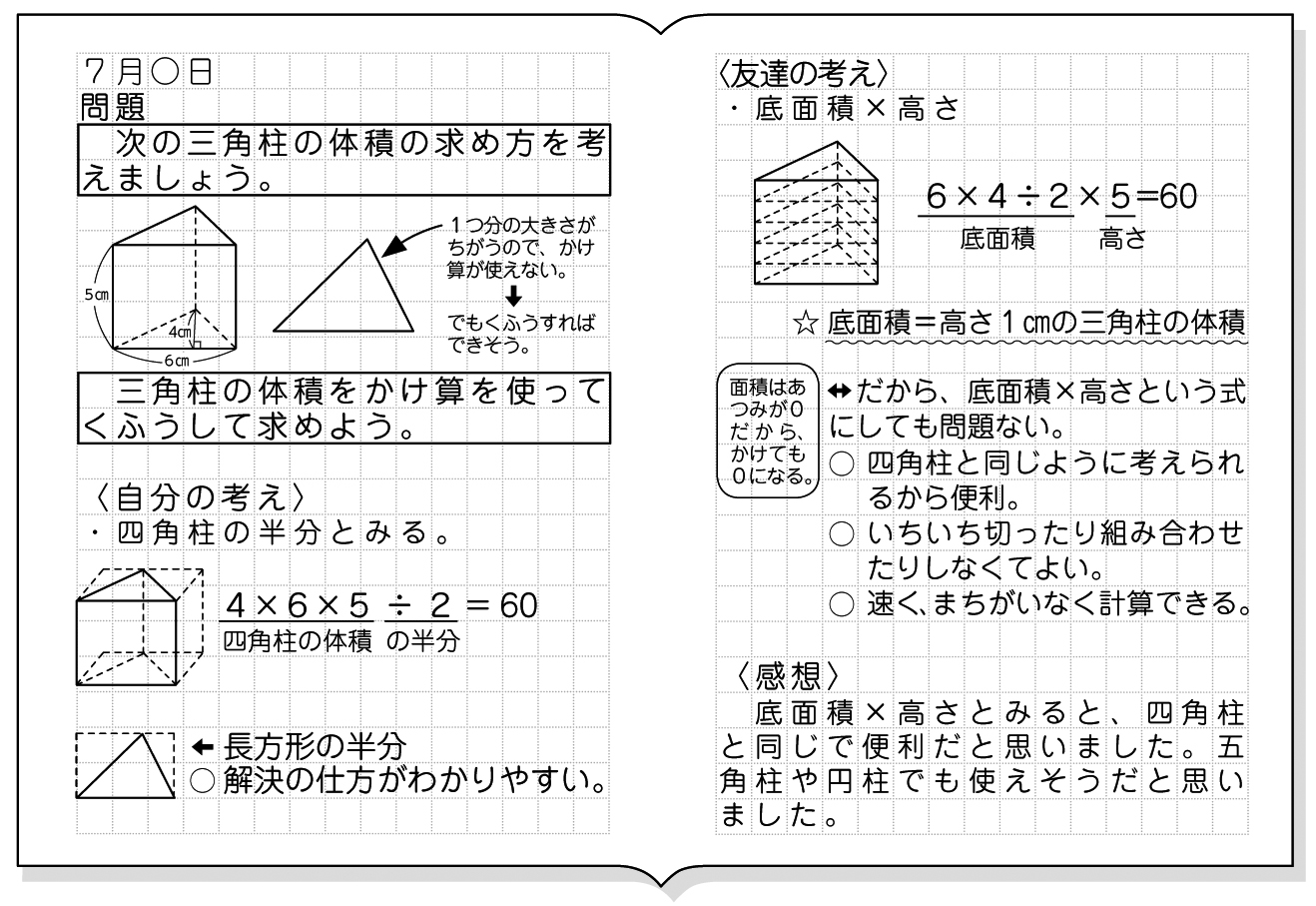
「皆さんどうも!今回は初めての授業ノート公開です!(o´Д`)緊張しますが良ければコメント、フォロー等よろしくお願いします!(*´ω`*) ちなみに余談ですが主は最高でも黒と赤と青しか基本使わない主義です。(大事なところが分からなくなってしまう)」, キーワード 算数,小6,角柱の体 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle





0 件のコメント:
コメントを投稿